Stabilized Bases for High-Order, Interpolation Semi-Lagrangian, Element-Based Tracer Transport
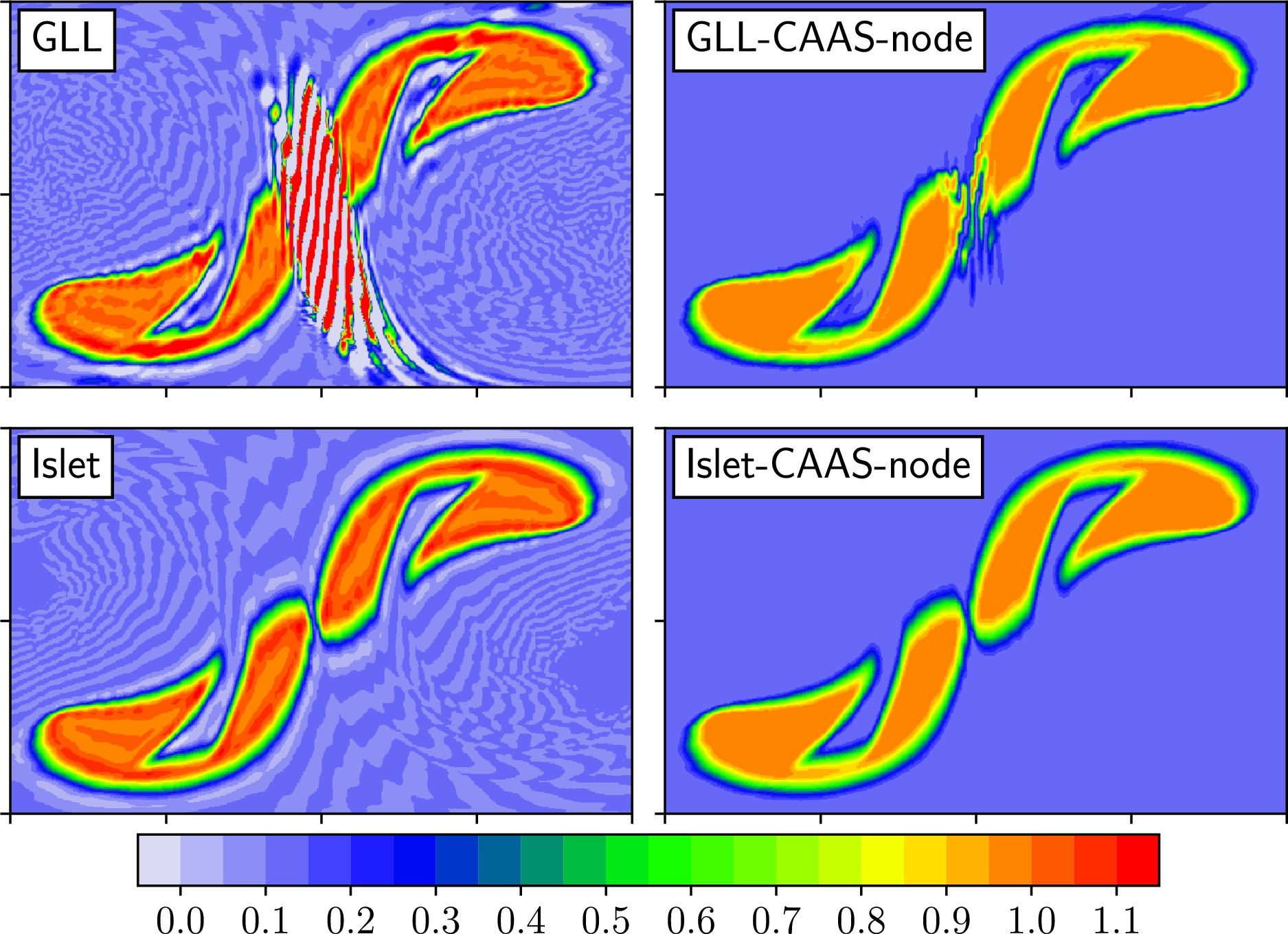
Figure 1. Images for unstable (top) and stable (bottom) interpolation semi-Lagrangian (ISL) transport showing tracer state near the end of a deformational flow in tracer transport test case. Top: Interpolation using the natural element basis leads to instability, seen here as oscillations in the tracer field. Bottom: Using the new Islet bases yields a stable solution. Left: No property preservation. Right: Shape preservation and global mass conservation are enabled. Also see Figure 2 in Islet: Interpolation Semi-Lagrangian Element-Based Transport.
Extremely efficient tracer transport is enabled by a new method to find stabilized element bases.
The Science
Advection of trace species, or tracers, also called tracer transport (Fig. 1), in models of the atmosphere and other physical domains is an important and potentially computationally expensive part of a model’s dynamical core. Tracers are used in models of atmospheric microphysics and macrophysics, convection, aerosols, and chemistry. Atmosphere models may use anywhere from a few to hundreds of tracers. It is therefore important that tracer transport be computed extremely efficiently.
Semi-Lagrangian (SL) advection methods are efficient because they permit a time step much larger than the advective stability limit for explicit Eulerian methods without requiring the solution of a globally coupled system of equations as implicit Eulerian methods do. Thus, to reduce the computational expense of tracer transport, dynamical cores often use SL methods to advect tracers.
The Impact
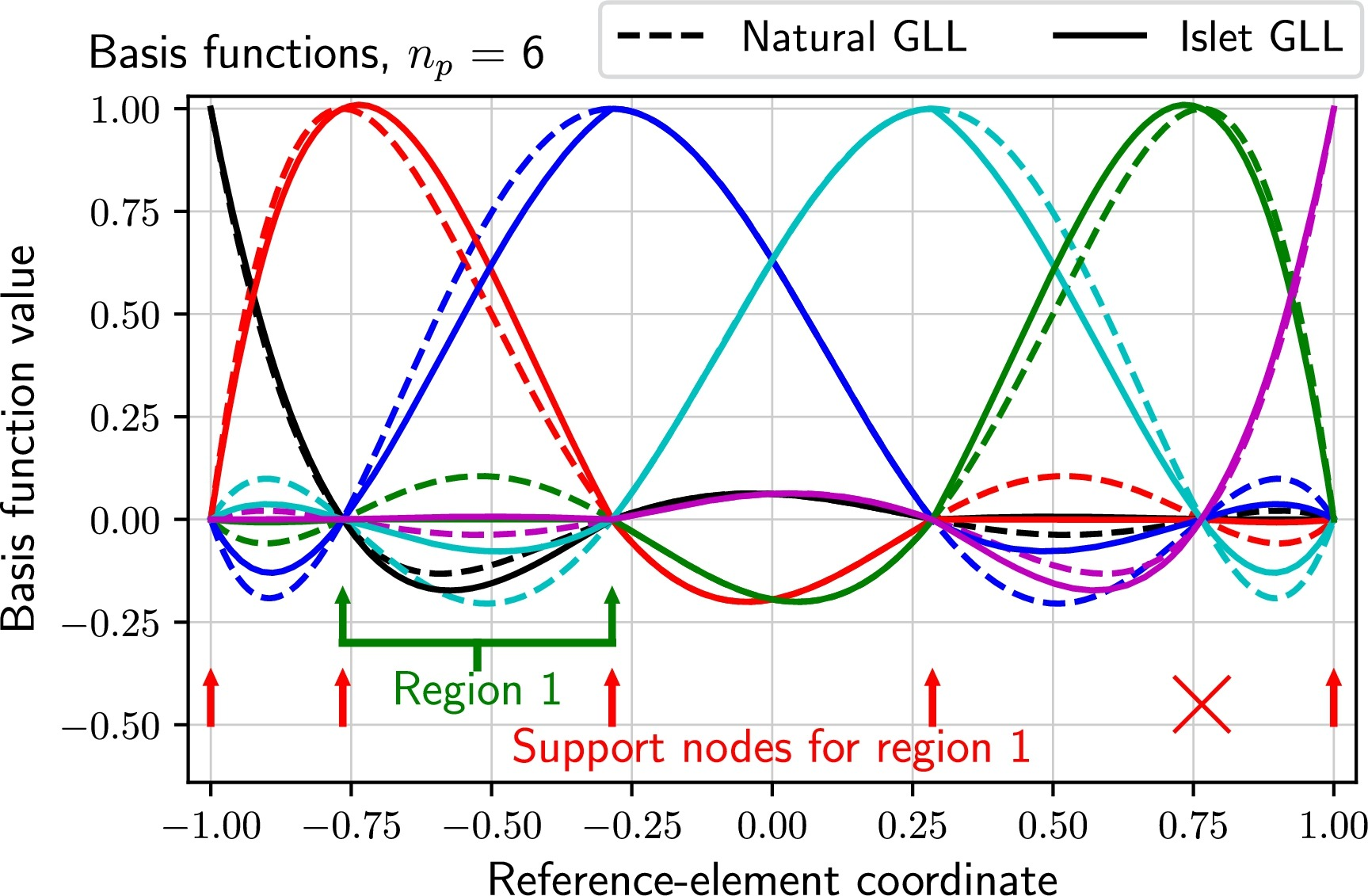
As part of developing a method that they call the Interpolation Semi-Lagrangian Element-based Transport (Islet) method, which is used in the E3SM Atmosphere Model (EAM), the researchers developed a new procedure to find stabilized interpolation semi-Lagrangian (ISL) basis sets (Fig. 2). These enable efficient ISL transport on unstructured element grids. The lowest-order Islet basis set is used in the EAM versions 2 and 3. It is part of a method that speeds up atmosphere tracer transport over version 1 by a factor of six to eight and provides a slightly higher resolution.
Figure 2. Natural (dashed lines) and new Islet basis functions (solid lines). Each basis function is a separate color. The Islet basis functions are constructed by modifying the natural basis functions. These modifications stabilize the element-based interpolation semi-Lagrangian method.
Summary
The class of ISL methods contains potentially extremely efficient SL methods. However, unstructured grids, such as those used by E3SM, are a challenge for ISL methods. The researchers developed an element-based ISL transport method that they call the Interpolation Semi-Lagrangian Element-based Transport (Islet) method, which can be applied to atmosphere models discretized using unstructured element-based methods, including the EAM. A core piece of the Islet method is a collection of element basis sets that provide spatial discretization. In contrast to classical ISL methods, the Islet method works on unstructured element grids. The natural element basis sets lead to an unstable ISL method. The researchers developed a procedure to search for modified, stabilized basis sets. The resulting basis sets provide extremely accurate tracer transport and excellent diagnostic values in a number of verification problems.
Publication
- Bradley, Andrew M. 2024. “Stabilized Bases For High-Order, Interpolation Semi-Lagrangian, Element-Based Tracer Transport”. Journal Of Computational Physics 508. Elsevier BV: 113034. doi:10.1016/j.jcp.2024.113034.
Funding
- This work was supported by the US Department of Energy (DOE) Office of Science’s Advanced Scientific Computing Research (ASCR) and Biological and Environmental Research (BER) Programs under the Scientific Discovery through Advanced Computing (SciDAC 4) ASCR/BER Partnership Program, and by the Energy Exascale Earth System Model (E3SM) project, funded by BER.
Contact
- Andrew M. Bradley, Sandia National Laboratories (SNL)
This article is a part of the E3SM “Floating Points” Newsletter, to read the full Newsletter check:
