New Physgrid and Dycore Methods Speed Up EAM by 2x

Figure 1. Left: Representation of the “ne4np4” cubed-sphere grid overlaid on the Earth. The ne4np4 grid has 4×4 spectral elements (shown as blue lines) in each cube face (the “ne” value, which is 4 here), and each spectral element (blue square) has a grid of green 4×4 Gauss-Lobatto-Legendre (GLL) points associated with it (the “np” value). During modeling, all variables are carried around on the GLL nodes. Right: A single 4×4 GLL Spectral Element (SE) depicted by blue lines (spectral element) and green closed circles (GLL points), overlaid by the 2×2 physics grid cells (pg2) within the element shown as red dashed lines and red open circles. The blue/green and red grids together compose the np4-pg2 dynamics-physics grid element in EAMv2. The blue and red lines are, in reality, on top of each other but are shown as adjacent for illustration purposes.
Background
An important element of the E3SM project is to improve computational performance of the model in order to enable high-resolution and ensemble simulations to address scientific questions. This article outlines recent efforts to improve the computational performance of the E3SM Atmosphere Model (EAM).
The E3SM Atmosphere Model consists of the High-Order Methods Modeling Environment (HOMME) Spectral Element dynamical core (dycore) and the EAM physics and chemistry parameterizations. In EAM version 1 (EAMv1), tracer transport is the most computationally expensive part of the dycore, and in low resolution simulations, parameterizations are more computationally expensive than the dycore. For EAM version 2 (EAMv2), two related efforts together provide an approximately two times (2x) speedup to EAM: high-order, property-preserving semi-Lagrangian tracer transport (“SL transport”) and high-order, property-preserving dynamics-physics-grid remap (“Physgrid”). SL transport and Physgrid work seamlessly both in the standard EAM configuration and in the Regionally Refined Mesh (RRM) configuration. The RRM configuration is an important EAM capability in which geographic regions of interest are resolved at higher resolution than the rest of the earth.
In EAMv1, physics and other parameterizations were computed at each grid point of the spectral element (SE) grid. In EAMv2, parameterizations are computed on a separate physics grid and quantities are remapped between the SE dynamics grid and the physics grid. Figure 1 illustrates these two grids within one horizontal spectral element. The green solid circles are Gauss-Lobatto-Legendre (GLL) spectral element grid points, which are used by the dycore. These 16 grid points correspond to the standard dynamics “np4” grid configuration, in which each spectral element’s internal grid is 4×4. The red dashed lines outline four EAMv2 physics finite volume (FV) cells within the spectral element. The open red circles mark the FV cell centers, which correspond to the new “pg2” physics grid configuration. Together, the green and red points illustrate the np4-pg2 dynamics-physics-grid configuration. In EAMv1, the physics FV grid is complicated: cell centers are on top of the GLL points, and some cells span multiple spectral elements. The EAMv1 grid is called the “np4-np4” dynamics-physics grid configuration. The np4-np4 configuration requires no remap algorithm to map fields between dynamics and physics grids. However, since there are approximately 4/9 as many unique physics grid points in an np4-pg2 EAMv2 simulation as in an np4-np4 EAMv1 simulation, EAMv2 simulations experience an over 2x speedup in the parameterizations. (The factor 4/9 is derived as follows. Each np4-pg2 element has 4 physics FV cells, providing the numerator. A spectral element shares boundary GLL grid points with its neighbors. Thus, in the EAMv1 np4-np4 configuration, sharing of boundary grid points leads to approximately 9 unique physics FV cells per spectral element, providing the denominator.)
Approach

Figure 2. Convergence test of high-order, property-preserving dynamics-physics-grid remap algorithms. np4-pg2 remap has an order of accuracy of 2, and np4-pg3 has an order of accuracy of 3.
EAMv2 algorithms are based on those described in Bosler et al. (2019) and Bradley et al. (2019), including cell-integrated remap, interpolation remap, and efficient global and local property preservation. SL transport in general has an up-front cost that must be amortized over multiple tracers. EAMv2 SL transport is extremely fast: it breaks even with EAMv1 Eulerian tracer transport at just 1-2 tracers and is 3-6x faster, depending on architecture, than Eulerian transport at 40 tracers, the number of tracers in the EAMv1 and v2 models.
For comparison, the Community Atmosphere Model (CAM) offers a different implementation of the “Physgrid” np4-pg2 dynamics-physics-grid configuration (Herrington et al., 2019) and SL transport (Lauritzen et al., 2017). CAM’s SL transport method breaks even with Eulerian transport at approximately 12 tracers and is about 1.7x faster at 40 tracers (Lauritzen et al., 2017). CAM’s “Physgrid” and SL transport methods do not yet work for RRM grids.
Before a new E3SMv2 feature is approved, it goes through a code review process which includes verification, validation, and performance testing. Figure 2 shows results of a convergence test of the Physgrid method. In a convergence test, a test field is remapped from the SE dynamics grid, to the physics grid, and then back to the SE dynamics grid. This is repeated for a sequence of increasingly fine meshes. On each mesh, the final, remapped field is measured against the original field. Each remap step conserves mass and preserves shape in each element (Bradley et al., 2019). As the mesh is refined, the accuracy of the np4-pg2 configuration increases with an order of accuracy of 2; np4-pg3, with an order of accuracy of 3. An order of accuracy of 1 means that the result is two times more accurate each time the mesh resolution is doubled; an order of accuracy of 2 is four times more accurate; order of accuracy 3 is eight times. In the context of a whole-Earth simulator, an order of accuracy of 2 or better is considered high order because many error sources have an order of accuracy of just 1. This verification test in addition to related climatology validation via E3SM diagnostics analysis and the Physgrid + SL transport performance gain make np4-pg2 the recommended configuration for EAMv2.
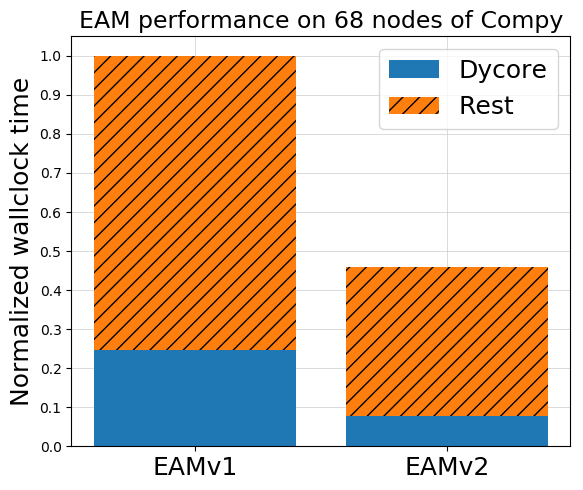
Figure 3. Performance results for the 1-degree atmosphere simulation run on 68 nodes of Compy. The EAMv1 total wallclock time is normalized to 1. The blue solid component, labeled “Dycore,” accounts for dynamics and tracer transport. The orange striped component, “Rest,” accounts for parameterizations, file I/O, land component, data components, and coupler. SL transport speeds up the Dycore component, and Physgrid speeds up the Rest component.
Impact
Together, high-order, property-preserving, Physgrid and SL transport speed up EAM by approximately 2x, roughly independent of architecture and workload per node. For example, Figure 3 shows performance results for a low-resolution atmosphere simulation run on 68 nodes of DOE’s Earth and Environmental System Modeling Compy compute cluster. The EAMv1 total wallclock time is normalized to 1. The blue solid component, labeled “Dycore,” accounts for dynamics and tracer transport. The orange striped component, “Rest,” accounts for parameterizations, file I/O, land component, data components, and coupler. EAMv2’s Dycore component is more than 3x faster than EAMv1’s, and EAMv2’s Rest component is almost 2x faster; together, these speed up EAM by more than 2x, allowing scientists to complete model runs in less than half the time of prior runs.

Figure 4. Top: CONUS 1/4-degree RRM grid. Bottom: Specific humidity at approximately 600 mbar on day 25 from DCMIP 2016 Test 1: Moist Baroclinic Instability on the CONUS 1/4-degree RRM grid. Bottom-left: Specific humidity from EAMv1 Eulerian transport and np4-np4 dynamics-physics-grid configuration. Bottom-right: Specific humidity from EAMv2 semi-Lagrangian transport and np4-pg2 dynamics-physics-grid (Physgrid) configuration.
E3SMv2 science will rely on the Regionally Refined Mesh to increase resolution in specific regions of interest, so it is imperative that E3SM’s new algorithms work in this configuration. Figure 4 illustrates the RRM capability of these algorithms. It shows specific humidity at approximately 600 mbar on day 25 from the DCMIP 2016 Test 1: Moist Baroclinic Instability on the CONUS 1/4-degree RRM grid. The map shows where grid resolution is increased. The left specific humidity image is for a simulation using EAMv1 Eulerian transport and the np4-np4 dynamics-physics-grid configuration. The right specific humidity image is for a simulation using EAMv2 semi-Lagrangian transport and the np4-pg2 dynamics-physics-grid (Physgrid) configuration. The EAMv2 configuration produces nearly identical results despite using much more efficient algorithms.
Multiple teams have contributed to this work, including the Exascale Computing Project’s E3SM-Multiscale Modeling Framework (ECP’s E3SM-MMF), the NH-MMCDG SciDAC, and E3SM’s Next Generation Development (NGD) Software & Algorithms, Performance, Water Cycle v2 Integration, and SCREAM teams.
Related News Article
References
- Bosler, P.A., Bradley, A.M., & Taylor, M.A. (2019). Conservative multimoment transport along characteristics for discontinuous Galerkin methods. SIAM Journal of Scientific Computing, 41(4), B870—B902. https://doi.org/10.1137/18m1165943
- Bradley, A.M., Bosler, P.A., Guba, O., & Taylor, M.A., & Barnett, G.A. (2019). Communication-efficient property preservation in tracer transport. SIAM Journal Scientific Computing, 41(3), C161–C193. https://doi.org/10.1137/18M1165414
- Herrington, A. R., Lauritzen, P. H., Reed, K. A., Goldhaber, S., & Eaton, B. E. (2019). Exploring a Lower‐Resolution Physics Grid in CAM‐SE‐CSLAM. Journal of Advances in Modeling Earth Systems. https://doi.org/10.1029/2019MS001684
- Lauritzen, P. H., Taylor, M. A., Overfelt, J., Ullrich, P. A., Nair, R. D., Goldhaber, S., & Kelly, R. (2017). CAM-SE–CSLAM: Consistent coupling of a conservative semi-Lagrangian finite-volume method with spectral element dynamics. Monthly Weather Review, 145(3), 833-855. https://doi.org/10.1175/MWR-D-16-0258.1
Funding
- Advanced Scientific Computing Research
- Climate Model Development and Validation
- Earth System Model Development
- Exascale Computing Project
- Scientific Discovery through Advanced Computing
Contact
- Andrew M. Bradley, Sandia National Laboratories
- Walter Hannah, Lawrence Livermore National Laboratory


