HOMME Non-Hydrostatic Dycore at 3 km Resolution Achieves 0.97 SYPD on Summit
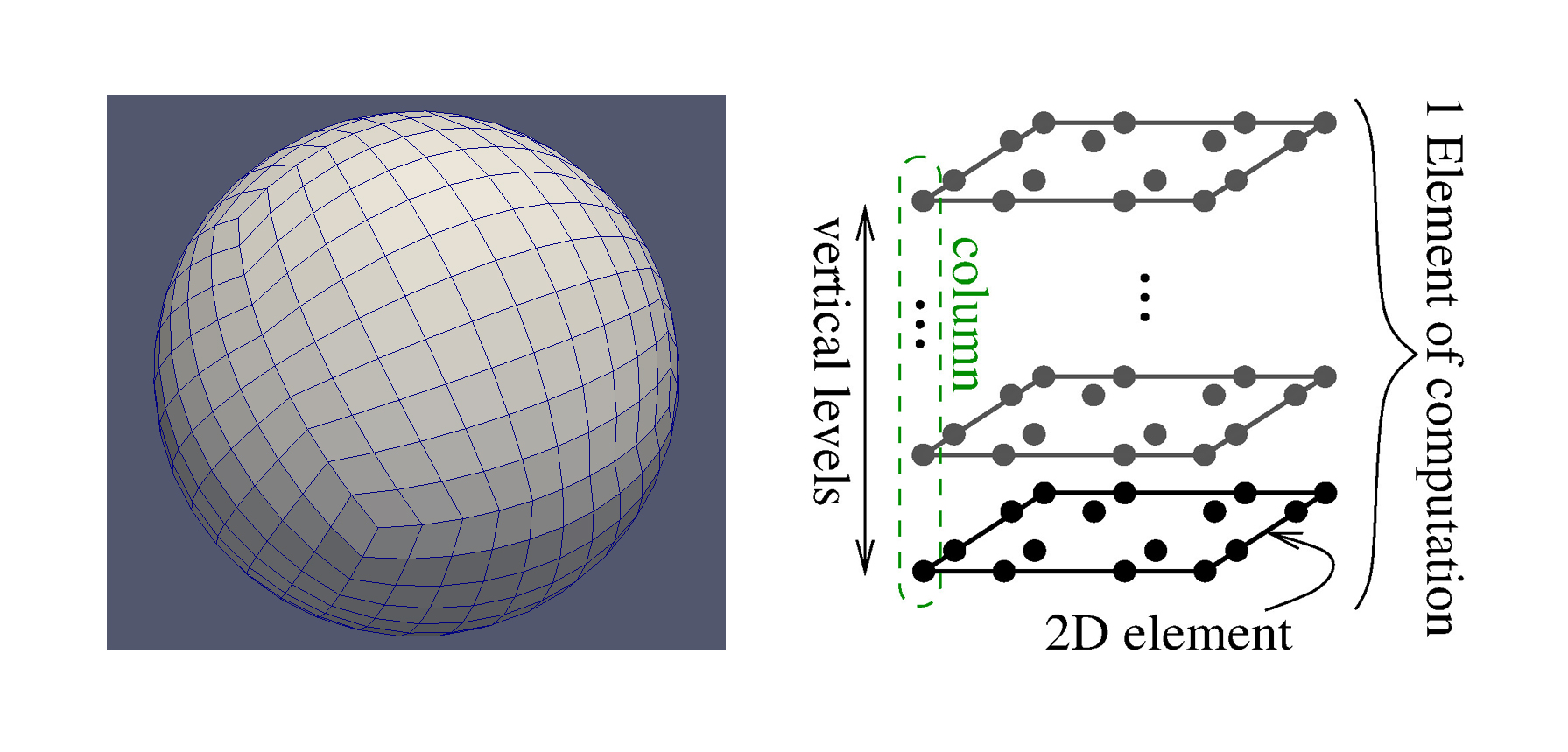
Figure 1. Left: Example of a 2D cubed-sphere mesh used in HOMME. Right: Depiction of a vertically extruded mesh element in HOMME. The 2D square element contains an N-by-N grid of points, corresponding to the Gauss-Legendre-Lobatto (GLL) points of the Spectral Element Method, and is vertically extruded for a given number of vertical levels.
Background
Climate models uniformly agree on the anthropogenic causes of global warming, but disagree on important details such as how much warming, how quickly it will occur, and changes in the frequency of extreme events. Reducing the uncertainty in global climate simulations is one of the grand challenges for the climate modeling community. One of the major sources of uncertainty is due to the parameterized effects of convective cloud systems. Current climate models are run at horizontal resolutions (i.e., average grid spacing at the Equator) as fine as 25 km, which still require the effects of these cloud systems to be approximated by parameterizations. Resolving these cloud systems starts to become possible at grid spacings in the range of 1-3 km.
The Simple Cloud-Resolving E3SM Atmosphere Model (SCREAM) project is focused on decreasing uncertainty by developing a global climate model tailored for these resolutions (1-3 km), i.e. creating a Global Cloud-Resolving Model (GCRM). At this scale, there are more grid cells and it is best for the atmospheric model to use a non-hydrostatic dynamical core rather than a simpler hydrostatic core. Both of these factors increase the number of unknowns to be calculated, which directly translates into an increase in computational cost.
In climate modeling, it is common to measure the performance of a model in terms of Simulated Days Per Day (SDPD) or Simulated Years Per Day (SYPD), which means the amount of days (or years) the model can forecast when allowed to run for a full day (24 hours) on a particular supercomputer. Given the increased cost of higher resolution models, science campaigns need the fastest SYPD throughput they can achieve.
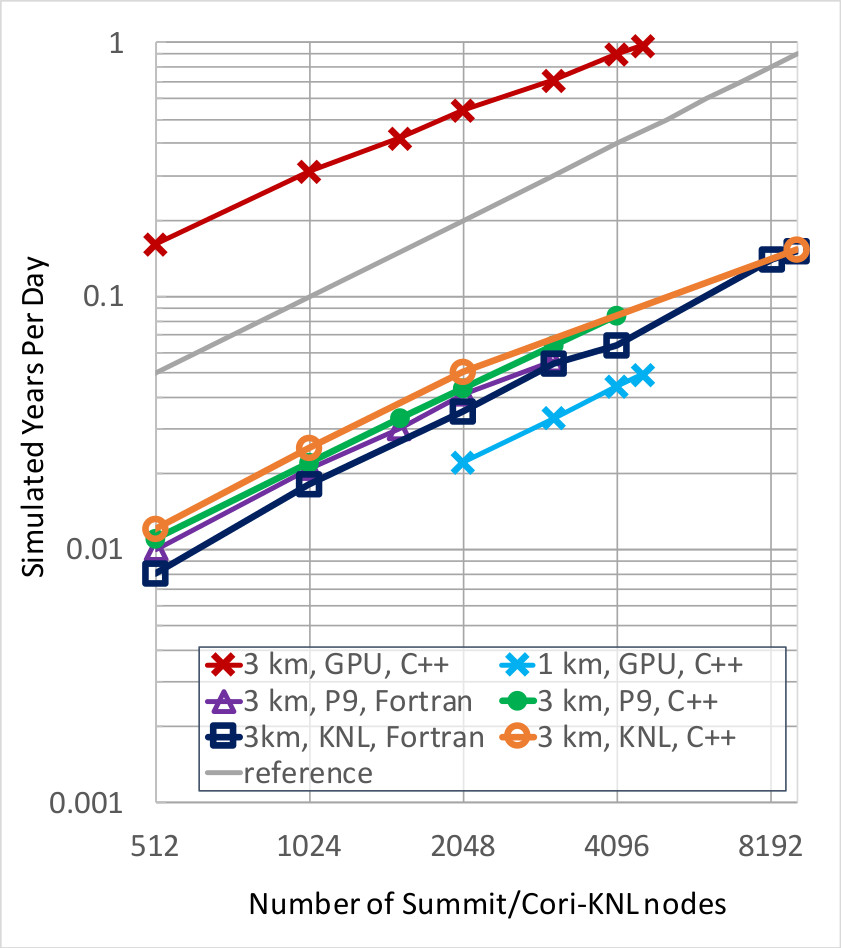
Figure 2. End-to-end scaling study comparing HOMMEXX-NH (C++) and HOMME-NH (Fortran) on target architectures for the 3 km resolution Next Generation Global Prediction System (NGGPS) benchmark, as well as for the 1 km benchmark (GPU only). All curves show excellent scaling, with some deterioration when reaching the full system size. As a reference, the gray line corresponds to perfect scaling.
The Performance Portability Challenge
The throughput requirement for a GCRM puts great emphasis on the code performance. In particular, the code needs to effectively use current state-of-the-art computing architectures and be capable of adapting to utilize whatever architectures will be available in tomorrow’s supercomputers. This challenge is usually referred to as performance portability. The challenge is often twofold: on one hand, the code needs to efficiently exploit all computational resources; on the other hand, the code should be maintained with reasonably small effort. The second requirement implies that the implementation should minimize as much as possible architecture-specific code (e.g., CUDA, HIP, SYCL) that can only be used on specific architectures.
Currently, there are several paradigms to achieve a performance-portable code, and minimize architecture-specific code. Each paradigm usually falls into one of the following categories:
- Compiler directives: compiler directives (or pragmas) are used to specify how the code should be compiled. This approach is usually fast to implement, but may lead to code duplication.
- General-purpose libraries: virtually all the architecture-specific choices and optimizations are delegated to an external library, maintaining a single interface in the code base. This approach helps to hide some technical performance optimization aspects while still leaving enough room for ad-hoc tuning, but might require some additional wrappers/interfaces for the external library.
- Domain-specific languages: the code is written in a new language, which an intermediate compiler then translates to general source code (such as Fortran or C++), performing optimizations on the basis of the underlying architecture. This approach hides virtually all the performance aspects, making the code more amenable for domain scientists, but may limit the ability to perform ad-hoc optimizations when needed.
In E3SM, the compiler directive approach for performance portability had been the dominant one for several years, notably through the use of OpenMP and OpenACC. The C++ library Kokkos (Edwards, Trott and Sunderland, 2014), which falls in the second category, has recently been put to the test as a potential solution to the performance-portability challenge. In Bertagna et al. (2019), Kokkos was used to obtain a portable implementation of the hydrostatic atmosphere dynamical core (dycore) of E3SM. In particular, the C++ rewrite of the hydrostatic dycore exploited Kokkos’s ability to nest parallelization levels in order to expose all the possible parallelism intrinsically existing in the mathematical algorithm. The resulting implementation was able to match or even outperform the original Fortran implementation on conventional CPU architectures, while also being efficient on GPUs. Performance portability was achieved.
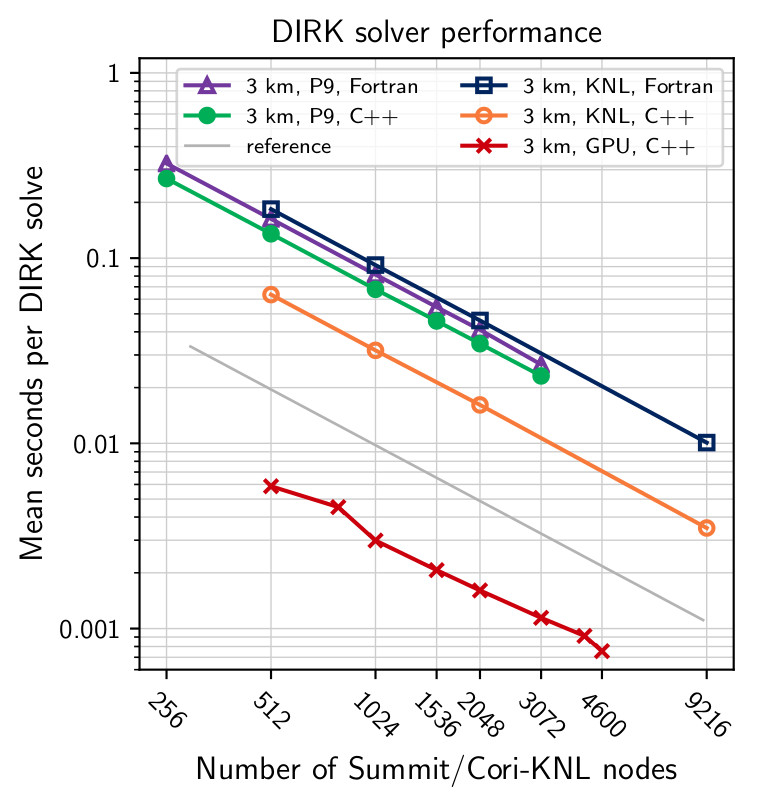
Figure 3. Scaling of the DIRK solver on target architectures for the 3 km NGGPS benchmark. All implementations scale perfectly, in part because this timer does not include any MPI communication costs. On KNL, HOMMEXX-NH substantially outperforms HOMME-NH because of the very efficient vectorization.
HOMME Non-Hydrostatic Dycore
The key to developing a GCRM is the atmosphere component, which consists of a dynamical core (dycore) and a set of physics parameterizations. In E3SM, the atmosphere dycore is given by the High-Order Methods Modeling Environment (HOMME), written in Fortran 90, which operates on 2D quadrilateral grids, vertically extruded for a configurable number of vertical levels. Figure 1 illustrates the structure of a vertically extruded element. HOMME decouples horizontal and vertical differential operators, using the Spectral Element Method (SEM) in the horizontal direction, and either Eulerian or Lagrangian methods in the vertical direction. HOMME provides a hydrostatic dycore, as well as a non-hydrostatic dycore. The former is a simplification of the the latter, and its use is widely accepted when the horizontal resolution is above those of a Cloud-Resolving Model (CRM), about 3 km. For the resolutions needed by a CRM, however, the latter non-hydrostatic dycore is usually preferred (Satoh et al., 2019), which means that, on top of the computational cost deriving from the increased resolution, a CRM also has to deal with increased complexity in the model itself.
In HOMME, the non-hydrostatic dycore solves for an arbitrary number of tracers, in addition to the state variables: horizontal velocity (a 2D vector quantity), potential temperature, pressure, geopotential, and vertical velocity. The timestepping uses a Horizontally-Explicit Vertically-Implicit (HEVI) approach. In particular, explicit Runge-Kutta (RK) schemes are used in the horizontal direction, while a Diagonally-Implicit Runge-Kutta (DIRK) scheme is used for the vertical direction, where a nonlinear equation involving geopotential and vertical velocity has to be solved several times in each time step.
The task of getting a performance-portable implementation of the non-hydrostatic dycore largely builds on the success of the hydrostatic dycore effort. When the two are compared, besides differences in the actual equations solved, scientists can identify two major additional challenges for the new non-hydrostatic dycore. The first is the need to solve a nonlinear equation in the DIRK scheme, for which developers use Newton’s method. Each column is independent of the others, and each Newton iteration requires the solution of a strictly diagonally dominant tridiagonal linear system in each column. Scientists exploited these facts in their effort to expose as much parallelism as possible. The second challenge is the management of temporary arrays, which stems from the increased resolution, as well as from algorithmic needs of the numerical scheme for the new model. This challenge required the implementation of careful memory allocation and management, which proved essential in GPU runs, in order to fit the problem in memory on a limited number of nodes.
Results
Scientists performed an extensive scalability study for the existing and new implementation of the non-hydrostatic dycores, on a variety of architectures. The systems used in the study were Summit and Cori. The former was used to test performance on both GPU and CPU architectures, using Nvidia V100 and IBM Power 9 (P9) architectures respectively, while the latter was used to test performance on the Intel Knights Landing (KNL) architecture. On P9 and KNL scientists ran both the existing non-hydrostatic (NH) Fortran implementation (HOMME-NH) as well as the new C++/Kokkos non-hydrostatic version (HOMMEXX-NH), while on GPU they only ran the new implementation. The following results are discussed in greater detail in a Supercomputing 2020 (SC ’20) proceedings paper (Bertagna et al., 2020).
Figure 2 shows the scaling of the dycore in terms of the SYPD metric. The runs were performed without any input/output (I/O), and setup time was not considered. Scientists ran the 3 km benchmark in the Next Generation Global Prediction System (NGGPS), which includes 10 tracers. Additionally, for GPU only, developers also ran the dycore at 1 km resolution, which yielded a problem with approximately 1 trillion degrees of freedom. On both benchmarks, HOMMEXX-NH (C++) shows excellent scaling, both on CPU and GPU, with HOMMEXX-NH slightly outperforming HOMME-NH (Fortran) on P9 and KNL architectures, because of the very efficient vectorization. For HOMMEXX-NH, the GPUs provide roughly a ten times (10x) speedup compared to KNL, and a twenty times (20x) speedup compared to P9. When scaling the application to the full Summit system (over 27,000 GPUs), HOMMEXX-NH is able to achieve 0.97 SYPD.
Figure 3 shows the scaling of just the DIRK solver, for the 3 km NGGPS benchmark. First, speedups are consistent with the whole application scaling study shown in Figure 2, with the GPUs providing roughly a 10x speedup compared to KNL and 20x speedup compared to P9. Second, HOMMEXX-NH is noticeably faster than HOMME-NH on P9 and more so on KNL (roughly by a factor of 1.2 on P9 and 2.8 on KNL).
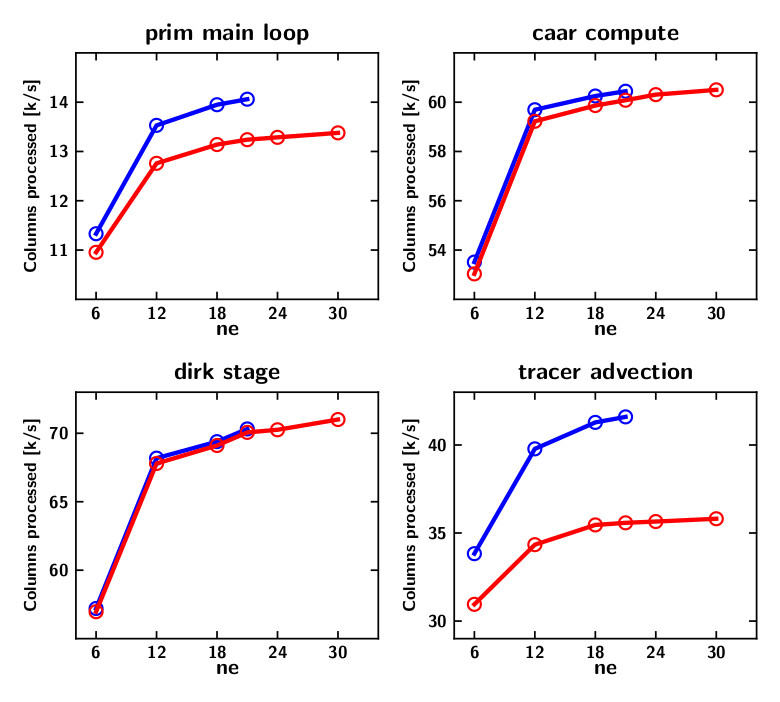
Figure 4. Single GPU performance of key HOMMEXX-NH kernels with (red) and without (blue) Workspace Manager (WSM). The number on the x-axis is directly linked to the total number of 2D elements, N, on the cubed sphere, by N=6*ne*ne, where “ne” is the number of spectral elements per cubed sphere edge. The y-axis reports the thousands of individual columns processed per second by the code. These simulations were run with 10 tracers.
Figure 4 shows the importance of carefully managing temporary arrays. In HOMMEXX-NH, the Workspace Manager (WSM) is the structure in charge of memory management. It is only enabled on GPU builds, and is responsible for allocating a minimal number of temporary arrays and to carefully distribute them to individual threads in the GPU. The plots show the performance of some key timers (in thousands of columns per second, k/s) with and without WSM enabled. The top left plot reports the performance of the entire application, while the remaining three show the performance of the three most important kernels. As the figure highlights, the WSM has a negative impact on performance, but the loss is relatively limited (less than 10% in the overall application), and WSM provides the benefit of fitting larger problems on the GPU. In the scaling studies reported in Figure 2, the 1 km benchmark would not fit in memory for the 2048 and 3072 node runs unless WSM was enabled. In a fully coupled E3SM simulation, scientists foresee the WSM being necessary also at 3 km resolution.
Impact on E3SM
The large throughput achieved by this work can have great impact on E3SM software development, as well as on researchers’ ability to answer key science questions. On the software development side, there currently is an increase in the use of Kokkos in several other E3SM-related projects, with several important design choices strongly influenced by the lessons learned in the development of HOMMEXX. On the science side, the performance-portable implementation of HOMMEXX, along with similar efforts for the physical parameterizations in SCREAM, are putting the ability to run decade-long cloud-resolving climate simulations within reach.
Publication
- L. Bertagna, O. Guba, M.A. Taylor, J.G. Foucar, J. Larkin, A.M. Bradley, S. Rajamanickam, A.G. Salinger, A Performance-Portable Nonhydrostatic Atmospheric Dycore for the Energy Exascale Earth System Model Running at Cloud-Resolving Resolutions, SC ’20: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Nov. 2020. (doi: 10.1109/SC41405.2020.00096)
Funding
- Climate Model Development and Validation
- Earth System Model Development
- Exascale Computing Project
Contacts
- Luca Bertagna and Oksana Guba, Sandia National Laboratories


