Surrogate Modeling and Machine Learning for Uncertainty Quantification

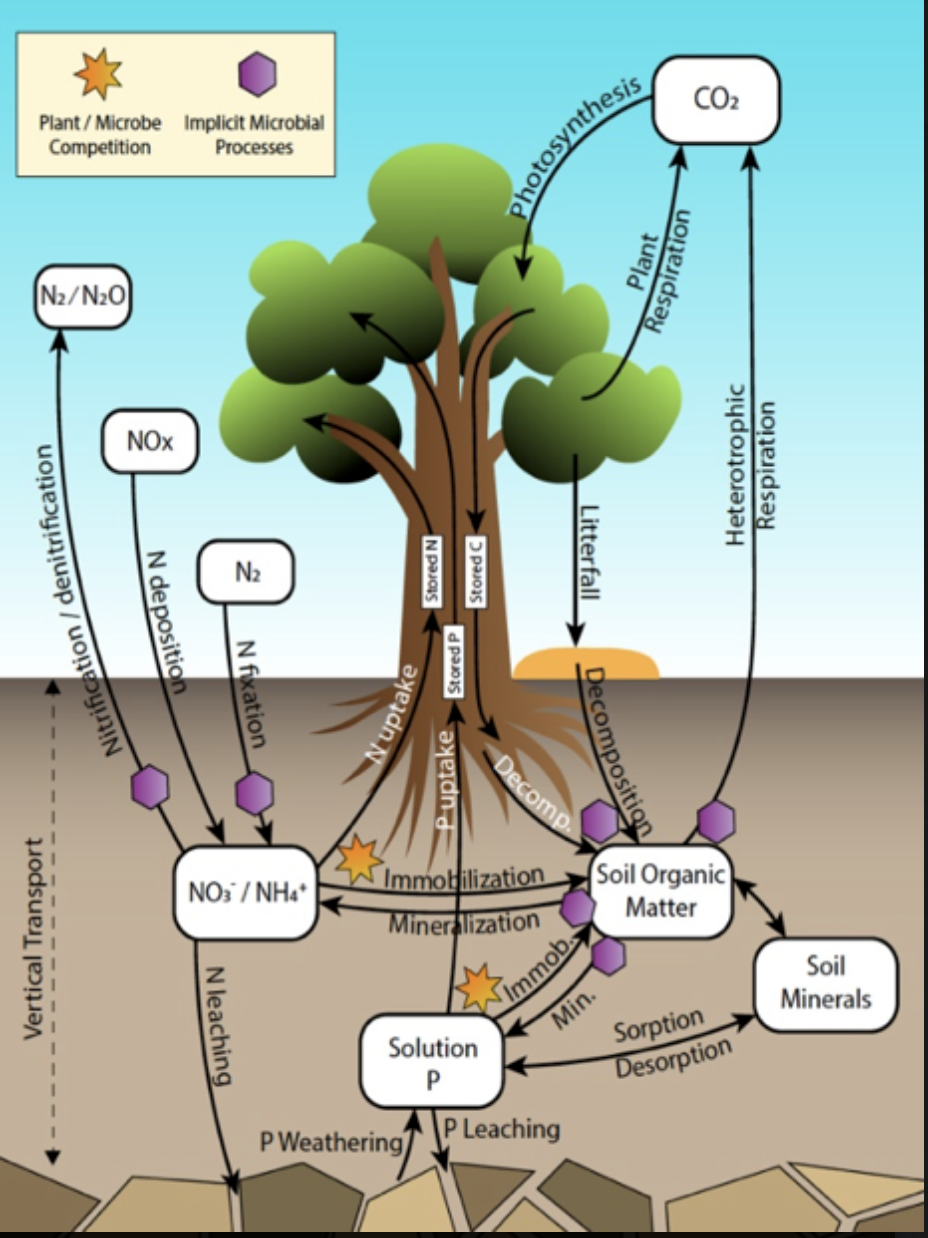
Figure 1: The representation of biogeochemical processes in the E3SM land model (ELM) that includes the cycling of carbon, nitrogen and phosphorus.

Quantifying uncertainty in E3SM using ensemble simulations is extremely expensive given the large number of uncertain parameters, model complexity and the computational cost of running simulations. The E3SM Land Model (ELM), a land component of E3SM, is a useful testbed for uncertainty quantification given the relatively lower computational expense compared to other components. ELM represents processes over the land surface associated with biogeochemistry (Fig. 1), along with hydrology, energy and land management. Despite the lower computational expense, model calibration or understanding the sensitivity of ELM outputs to parameter uncertainty is still prohibitively expensive when considering more than a few parameters at a time because the required number of model simulations grows exponentially with the number of uncertain parameters.  This limitation may be overcome by performing the large ensembles with surrogate models instead of the original model. Surrogate models, which may be constructed using analytical forms with machine learning approaches, are trained on a limited number of ELM simulations for the purpose of predicting ELM responses over any combination of parameter values within the specified ranges used for the training simulations. These surrogate models are much faster to evaluate than ELM, often by several orders of magnitude.

There are two key challenges in developing and applying surrogate models that may be addressed by machine learning. The first challenge is that traditionally, one must construct different surrogate models for each quantity of interest (e.g., the average latent heat flux during a particular month at a particular location). If a researcher is interested in global fields for multiple variables over an extended time period, the number of quantities of interest explodes into millions or billions, and the problem once again becomes computationally infeasible given the expense of constructing that many surrogate models. Second, the surrogate model must capture the model responses accurately enough to provide reliable results (e.g., parameter sensitivity analysis or model parameter calibration). The desire is to produce a surrogate model that is as accurate as possible with as few ELM simulations as possible. Threshold responses or other highly nonlinear model behavior may limit the potential accuracy of surrogate models.

In this study, scientists addressed these challenges in an example uncertainty quantification problem that explored the impact of ten uncertain parameters on simulated gross primary productivity (GPP). GPP represents the gross uptake of carbon by vegetation through photosynthetic processes. Researchers randomly varied these ten parameters over specified ranges of uncertainty and performed an ensemble of 200 ELM simulations at 1.9×2.5 degree resolution. Considering monthly GPP values over the period from 2000 to 2014 at this spatial resolution, there are half a million quantities of interest. To construct the surrogate model, scientists tested two methods that both exploit strong temporal and spatial correlation in model output fields by employing dimension reduction techniques. In the first approach, singular value decomposition (SVD) was used to reduce the dimensionality of the outputs. The results showed that ten principal components were sufficient to capture 97% of the variability of GPP over time and space. A neural network model was then trained on the ten principal components to produce a surrogate model. This approach reduced the complexity of the surrogate model by four orders of magnitude and thus greatly reduced the number of ELM simulations. These ten principal components were then back transformed to the GPP estimates at each location and time period for various combinations of the ten parameters. The surrogate model is very accurate, producing highly consistent simulation results with the ELM. In most cases, the coefficient of determination (R²) between the surrogate and the ELM simulations is greater than 0.95, close to the perfect match of 1.0. Lu and Ricciuto (2019) describes this surrogate modeling method, which was used to conduct a sensitivity analysis for globally averaged GPP, indicating the relative influence of model parameters and their interactions (Figure 2).

The second dimension reduction approach decomposed the high-dimensional spatio-temporal output in terms of Karhunen-Loève (KL) expansions, reducing the problem to the construction of about 150 surrogates instead of approximately half a million (3183 land cells over 180 months). Furthermore, each KL coefficient surrogate was formed using sparse polynomial chaos (PC), which allows exact recovery of output variance decomposition or global sensitivity analysis without additional surrogate sampling. The eventual KL-PC surrogate represents ELM over the whole globe within 5% relative root-mean-square error. Researchers are currently tuning the surrogate construction towards the highest possible accuracy in order to use it for model parameter calibration given global spatiotemporal GPP observations. The current surrogate, however, is sufficiently accurate to estimate parameter sensitivities over space and time with high confidence.

Scientists used this surrogate model to analyze the variations of parameter sensitivity over space and time (Figure 3).

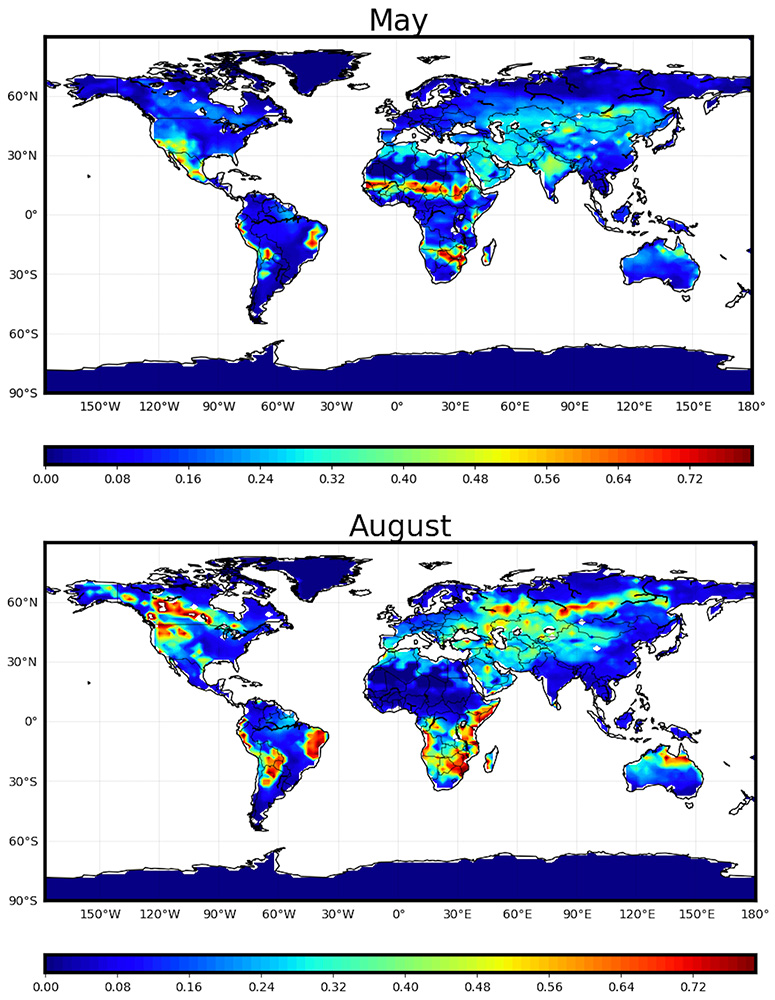
Figure 3:  Sensitivity of GPP to mbbopt, a parameter regulating stomatal conductance in leaves, in May and August averaged over the period 2000-2014. Although Figure 2 indicates flnr is the most sensitive parameter globally, mbbopt becomes more sensitive during seasonally dry or drought conditions, for example over the Sahel region in May or in boreal regions in August. Sensitivity analysis of spatially and temporally varying outputs yields important information about governing processes.

The high accuracy and successful application of these surrogate methods for ELM with limited numbers of training simulations imply that these methods may benefit other more expensive model components and the fully coupled model. In E3SM and related SciDAC ecosystem projects, scientists are researching methods to further improve the accuracy of surrogate modeling methods, especially those using deep learning. These surrogate models may also be used for calibration to minimize biases between simulated and observed quantities of interest. A near-term research goal is to use these surrogate models to improve model performance against benchmarks currently available through the International Land Model Benchmarking project (ILAMB). Estimates of prior and posterior model prediction uncertainty, which is important information for both scientists and policymakers, may also be derived from model ensembles and the surrogate models. Figure 4 shows the prior uncertainty (standard deviation) in GPP when considering 200 ELM ensemble members and the evolution of this uncertainty over time.

Figure 4: Animation of the standard deviation of gross primary productivity (GPP; gC/m2/day) over the 200 ensemble members, for 15 years. Higher standard deviations tend to be associated with higher mean values of GPP. In the mid and high latitudes of the Northern Hemisphere, a seasonal cycle is clearly evident with large values in the summer months and smaller values in the winter months.

Related Resources

E3SM All-Hands Presentation:

• Video recording on E3SM’s YouTube Channel
• PDF of presentation

Funding

• ESMD – E3SM Project (DOE BER)
• OSCM SciDAC (DOE BER and ASCR)
• Oak Ridge Terrestrial Ecosystem Sciences Scientific Focus Area (DOE BER)

Contacts

• Daniel Ricciuto and Dan Lu
  Oak Ridge National Laboratory
• Khachik Sargsyan
  Sandia National Laboratories