Radiocarbon Reconstruction Evaluated by the E3SM Land Model
An accurate reconstruction of soil radiocarbon demonstrated in ELMv1 can be used to compare CMIP6 models to global observations.
Radiocarbon (14C) is a powerful tracer of the global carbon cycle that is commonly used to assess carbon cycling rates in various Earth system reservoirs and as a benchmark to assess climate model performance. Therefore, it has been recommended that Earth System Models (ESMs) participating in the Coupled Model Intercomparison Project Phase 6 (CMIP6) report predict 14C values for relevant carbon pools. However, a detailed representation of 14C dynamics may be an impractical burden on model developers. In a recent Journal of Advances in Modeling Earth Systems (JAMES) paper, Metzler et al. (2020), scientists presented an alternative approach to compute 14C values from the numerical output of an ESM that does not explicitly represent these dynamics. Researchers evaluated their approach using the E3SM land model (ELMv1) (Chen et al., 2019; Zhu et al., 2019; Riley et al., 2018).
Background
Terrestrial ecosystems, and soils in particular, are important global carbon (C) reservoirs but have large uncertainties in the size of the stock, process rates, and their representation in Earth System Models. The dynamics of 14C in various components of terrestrial ecosystems can be used to interpret the rates at which (1) CO2 is removed from the atmosphere into plants through photosynthesis, (2) CO2 moves from vegetation into soils through litter fall and mortality, and (3) CO2 cycles back to the atmosphere via respiration. As a result, 14C has been used in many empirical studies to evaluate rates of soil C cycling and, more recently, as a tool for model evaluation (Ahrens et al., 2015; Chen et al., 2019; Dwivedi et al., 2017) and intercomparison (He et al., 2016).
Linear response theory suggests that the impulse response function of a particular model can be used to compute isotope dynamics without explicitly simulating the isotope within the model but rather using the response function to convolve the isotope tracers (Thompson & Randerson, 1999). Therefore, it may not be necessary to explicitly represent isotope dynamics a priori in a model; rather, they can be obtained a posteriori through the convolution procedure. However, linear response theory relies on assumptions of steady‐state and model linearity, which are not met for the type of transient simulations performed with ESMs.
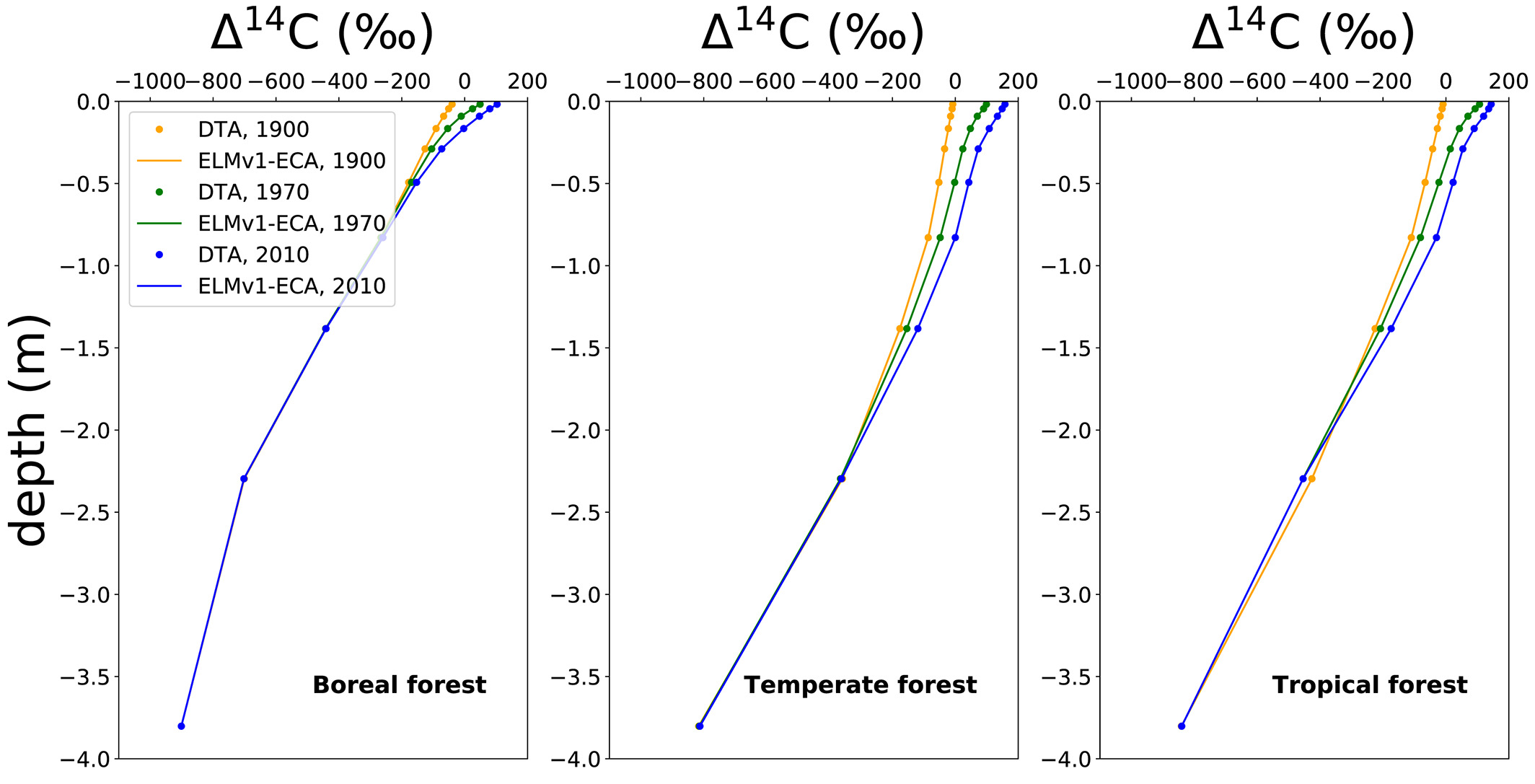
Discrete‐Time Approximation (DTA) using 10‐day time step and ELMv1‐ECA modeled Δ14C values with depth in 1900, 1970, and 2010. The mean absolute DTA bias is less than 0.001% for Δ14C in soils across all sites. Sites (left to right): boreal, temperate, and tropical. Δ14C values decrease with depth and become more enriched post‐1960s as they take up bomb‐derived 14C from the atmosphere.
Metzler et al. (2018) recently developed a method to obtain a mathematical object, the state‐transition matrix, which generalizes response function theory for nonlinear models out of equilibrium. This approach removes previous assumptions that prevented the use of the linear response approach for the computation of isotope and tracer dynamics a posteriori from simulations. Therefore, the state‐transition matrix approach offers an opportunity to compute isotope dynamics from models that do not explicitly represent them and could be applied to models participating in CMIP6, for example. Since output from these models is provided in discrete time steps often much larger than the internal model time step, it is a challenge to translate the state‐transition‐matrix approach from the continuous to the discrete case. In the recently-published Metzler et al. (2020) paper, however, scientists extended the Metzler et al. (2018) method to the discrete‐time case and applied it to reconstruct tracer and isotope dynamics from model output.
Approach
Carbon cycle models are subject to the law of mass conservation and therefore can be represented as compartmental systems. The JAMES paper approach required computed 12C stocks and fluxes among all carbon pools for a particular simulation of the model. From this output, a time‐dependent linear compartmental system was computed with its respective state‐transition matrix. Using transient atmospheric 14C values as inputs, the state‐transition matrix was then applied to compute 14C values for each pool, the average value for the entire system, and component fluxes.
Researchers demonstrated the approach with ELMv1‐ECA, an alternative version of E3SM’s land model that explicitly represents 12C and 14C in seven soil pools and 10 vertical layers, making it an appropriate test case to evaluate the proposed method.

Δ14C values in the different pools aggregated for all depths through time (Lines: ELMv1‐ECA; dots: DTA using 10‐day time step). Sites (top to bottom): boreal, temperate, and tropical forests. CWD is coarse woody debris. Litters 1, 2, and 3 denote metabolic, cellulose, and lignin litters. Soils 1, 2, and 3 are fast, intermediate, and passive soil pools. Atmospheric Δ14C values (blue) increase in response to nuclear bomb testing in the 1960s. Faster cycling pools respond more rapidly to the atmospheric Δ14C changes. Slower cycling pools show a lagged and damped response. Differences in DTA and ELMv1‐ECA modeled values are imperceptible in this figure.
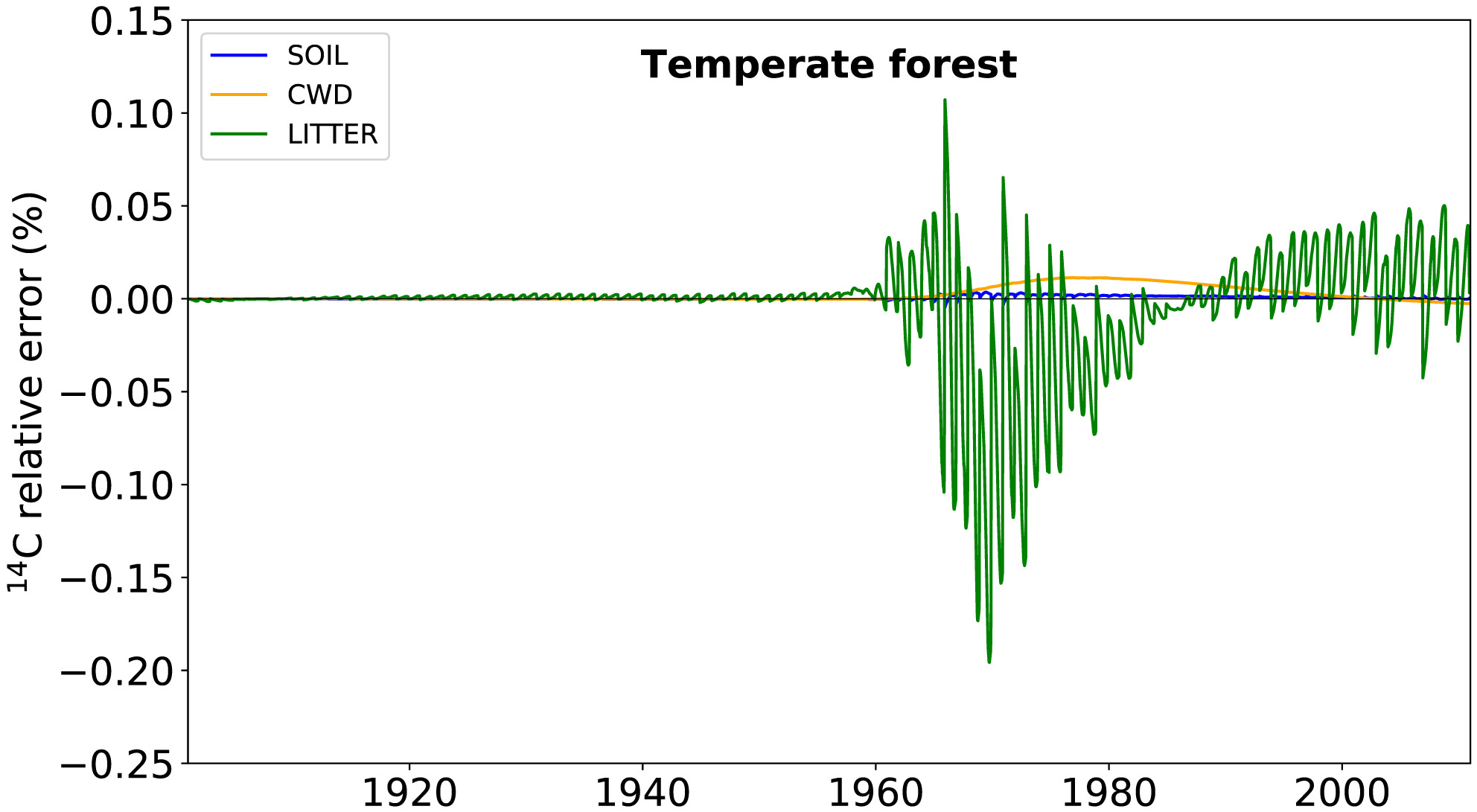
Relative error in 14C values for coarse woody debris (CWD), aggregated litter, and soil pools over time for the temperate forest site. 14C relative error is approximately two orders of magnitude larger than 12C error but is always small in comparison to model uncertainty and spatial heterogeneity (Chen et al., 2019; Lawrence et al., 2019). The largest biases in the litter pool follow the bomb spike in atmospheric 14C concentrations and vary seasonally.
Results
Results from the proposed method are highly accurate (relative error <0.01%) compared with the ELMv1‐ECA 12C and 14C predictions, demonstrating the potential to use this approach in CMIP6 and other model simulations that do not explicitly represent 14C. Since comparisons against observations indicate that ESM land models inaccurately predict soil carbon (C) turnover, this approach provides a framework to improve process representations affecting these biases.
Publication
- Metzler, H., Zhu, Q., Riley, W., Hoyt, A., Müller, M., & Sierra, C. (2020). Mathematical Reconstruction of Land Carbon Models From Their Numerical Output: Computing Soil Radiocarbon From C Dynamics. Journal of Advances in Modeling Earth Systems, 12(1). https://doi.org/10.1029/2019ms001776.
Additional References
- Holm, J. A., R. G. Knox, A. J. N. Lima, C. D. Koven, M. Longo, W. J. Riley, R. I. Negron-Juarez, A. C. d. Araujo, A. Manzi, L. M. Kueppers, P. R. Moorcroft, N. Higuchi, and J. Q. Chambers (2020), The Central Amazon forest sink under current and future atmospheric CO2: Predictions from big-leaf and demographic vegetation models, JGR-Biogeosciences, https://doi.org/10.1029/2019JG005500.
- Zhu, Q., W. J. Riley, C. M. Iversen, and J. Kattge (2020), Assessing impacts of plant stoichiometric traits on terrestrial ecosystem carbon accumulation using the E3SM land model, J. of Advances in Modeling Earth Systems, https://doi.org/10.1029/2019MS001841.
- Chen, J., Q. Zhu, W. J. Riley, Y. He, J. T. Randerson, and S. E. Trumebore (2019), Comparison with Global Soil Radiocarbon Observations Indicates Needed Carbon Cycle Improvements in the E3SM Land Model, JGR-Biogeosciences, https://doi.org/10.1029/2018JG004795.
- Zhu, Q., W. J. Riley, J. Y. Tang, J. R. Randerson, N. Collier, F. M. Hoffman, X. Yang, and G. Bisht (2019), Representing nitrogen, carbon, and phosphorus interactions in the ELMv1-ECA Land Model: Model development and global benchmarking, J. of Advances in Modeling Earth Systems, https://doi.org/10.1029/2018MS001571.
- Riley, W. J., Q. Zhu, and J. Y. Tang (2018), Weaker land-climate feedbacks from nutrient uptake during photosynthesis-inactive periods, Nature Climate Change, https://doi.org/10.1038/s41558-018-0325-4.
Funding
- The U.S. Department of Energy Office of Science, Biological and Environmental Research supported this research as part of the Earth System Model Development program area through the Energy Exascale Earth System Model (E3SM) project. Additional funding came from the Regional & Global Model Analysis program area through the Reducing Uncertainty in Biogeochemical Interactions through Synthesis and Computation (RUBISCO) Scientific Focus Area (SFA)
Contact
- William J. Riley, Lawrence Berkeley National Laboratory


