Applying a Mathematical Diagnostic Tool to Detect Numerical Pathologies in Atmospheric Physics Parameterizations
A success story of applying convergence testing to detect and address issues of numerical discretization in nonlinear representations of turbulence and clouds.
The Science
Numerical models can help researchers develop an understanding of atmospheric physics. Spatiotemporal discretization is a necessary step for translating mathematical equations to codes for supercomputers. Discretized models are expected to faithfully represent the underlying set of continuous equations, but this necessary condition is violated sometimes by subtle pathologies that have crept in during the discretization. Such pathologies can introduce undesirable artifacts, such as sawtooth noise in space and time, into the model solutions. Certain pathologies may cause non-negligible changes in the long-term statistics of the model behavior, giving misleading numerical results. In order to improve the trustworthiness of numerical models, it is important to detect and eliminate the presence of such pathologies.
In this study, computational scientists employed a diagnostic tool, called numerical convergence testing, to verify the discretization of the Cloud Layers Unified By Binormals (CLUBB) model of clouds and turbulence. Sophisticated atmospheric physics parameterizations like CLUBB are not usually subjected to convergence testing of numerical discretization, partly because of the arguable standpoint that numerical errors are less important than errors in model formulation, and partly because of the difficulty in identifying the cause of non-convergent results. However, guided by the convergence tests, the researchers identified and addressed issues in the numerical algorithms used in this physics parameterization, improving the overall fidelity of the results.
The Impact
When convergence testing suggests proper behavior, researchers can have more confidence that the numerical model, if it is run at adequate resolution, faithfully represents the physics described by the model equations. This is a necessary foundation for further work to increase numerical accuracy.
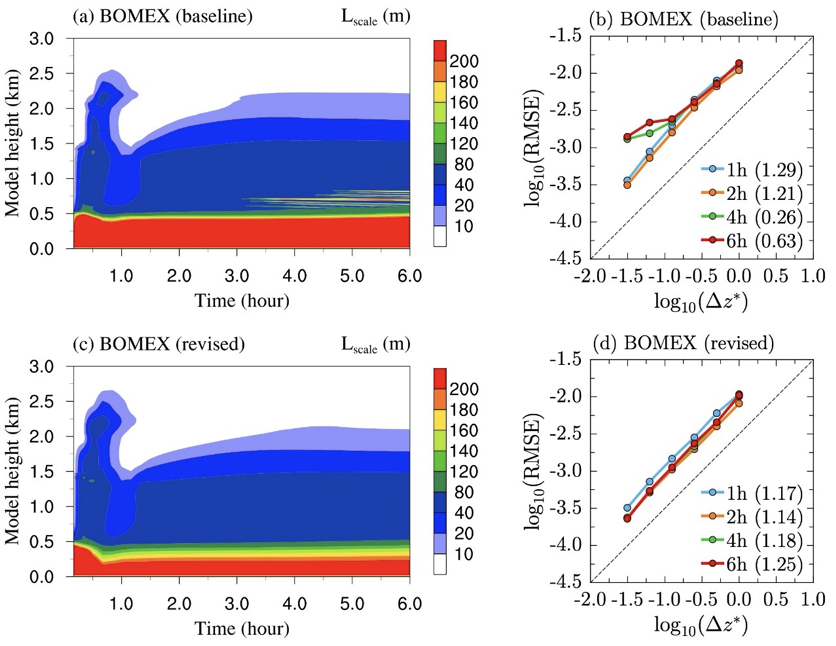
Figure 1. Numerical simulations of shallow cumulus clouds in the Barbados Oceanographic and Meteorological Experiment (BOMEX) single-column test case before (upper row) and after (lower row) numerical pathologies are addressed. Addressing the pathologies eliminates the nonphysical oscillations occuring at 0.5km – 1km altitudes between hours 3 and 6 seen in panel (a) and leads to results that exhibit the expected first-order convergence in panel (d).
Summary
Atmospheric physics parameterizations are simplified descriptions of physical and chemical processes that cost too much computing power to simulate in detail. Typically, parametrization development focuses on the formulation of underlying mathematical equations, rather than the numerical algorithms that solve those equations. Resolution convergence testing assesses the behavior of the numerical results by varying the resolution across a wide range.
In this study, convergence testing identifies two aspects of CLUBB’s equation set that contribute to undesirable noise in the solutions. First, numerical limiters (i.e., clipping) used by CLUBB introduce discontinuities or slope discontinuities in model fields. Second, nonlinear artificial diffusion employed for improving numerical stability can introduce unintended small-scale features into the solution of the model equations. Smoothing the limiters and using linear artificial diffusion reduces the noise and restores the expected first-order convergence in CLUBB’s solutions. These model reformulations enhance the confidence in the trustworthiness of solutions from CLUBB by eliminating the unphysical oscillations in high-resolution simulations, see Figure 1 for results from single-column simulations of the Barbados Oceanographic and Meteorological Experiment (BOMEX) test case. The improvements in the results at coarser, near-operational grid spacing and timestep are also seen in cumulus cloud and dry turbulence tests. Both the method of testing and the numerical issues detected are expected to be relevant to other atmospheric models.
Publication
- Zhang, S., C. J. Vogl, V. E. Larson, Q. M. Bui, H. Wan, P. J. Rasch, and C. S. Woodward. 2023. “Removing numerical pathologies in a turbulence parameterization through convergence testing.” Journal of Advances in Modeling Earth Systems, 15, e2023MS003633. [DOI: 10.1029/2023MS003633]
Funding
- This research has been supported by the Department of Energy’s Scientific Discovery through Advanced Computing (SciDAC) program via a partnership in Earth System Model Development between the Biological and Environmental Research (BER) and the Advanced Scientific Computing Research (ASCR) programs. Numerical simulations were carried out using the BER-funded Compy computing cluster located at Pacific Northwest National Laboratory and using the Livermore Computing Center at Lawrence Livermore National Laboratory.
Contact
- Hui Wan, Pacific Northwest National Laboratory
This article is a part of the E3SM “Floating Points” Newsletter, to read the full Newsletter check:



