A Scalable Implicit Time-Stepping Method for the E3SM Ocean Model
Figure 1. Strong scaling results for the barotropic mode solved by the explicit-subcycling scheme (the existing scheme; the blue solid) and the semi-implicit method (the new scheme; the red solid). The MPAS-O model was run on the National Energy Research Scientific Computing Center’s Cori supercomputer.
Science
Scientists have implemented the semi-implicit barotropic mode solver in the MPAS-O to allow faster and more stable simulation as a competitor of the existing split-explicit subcycling scheme. When implementing the semi-implicit method for any kind of numerical model, one of the most important issues is that the global collective process which requires all-to-all communication among cores should be called as infrequently as possible to achieve better scalability. The barotropic mode solver uses a pipelined preconditioned bi-conjugate gradient method with the restricted additive Schwarz preconditioner, where the preconditioner helps to accelerate the convergence of the iterative solver and therefore decrease the number of the global collective process up to 90%.
Impact
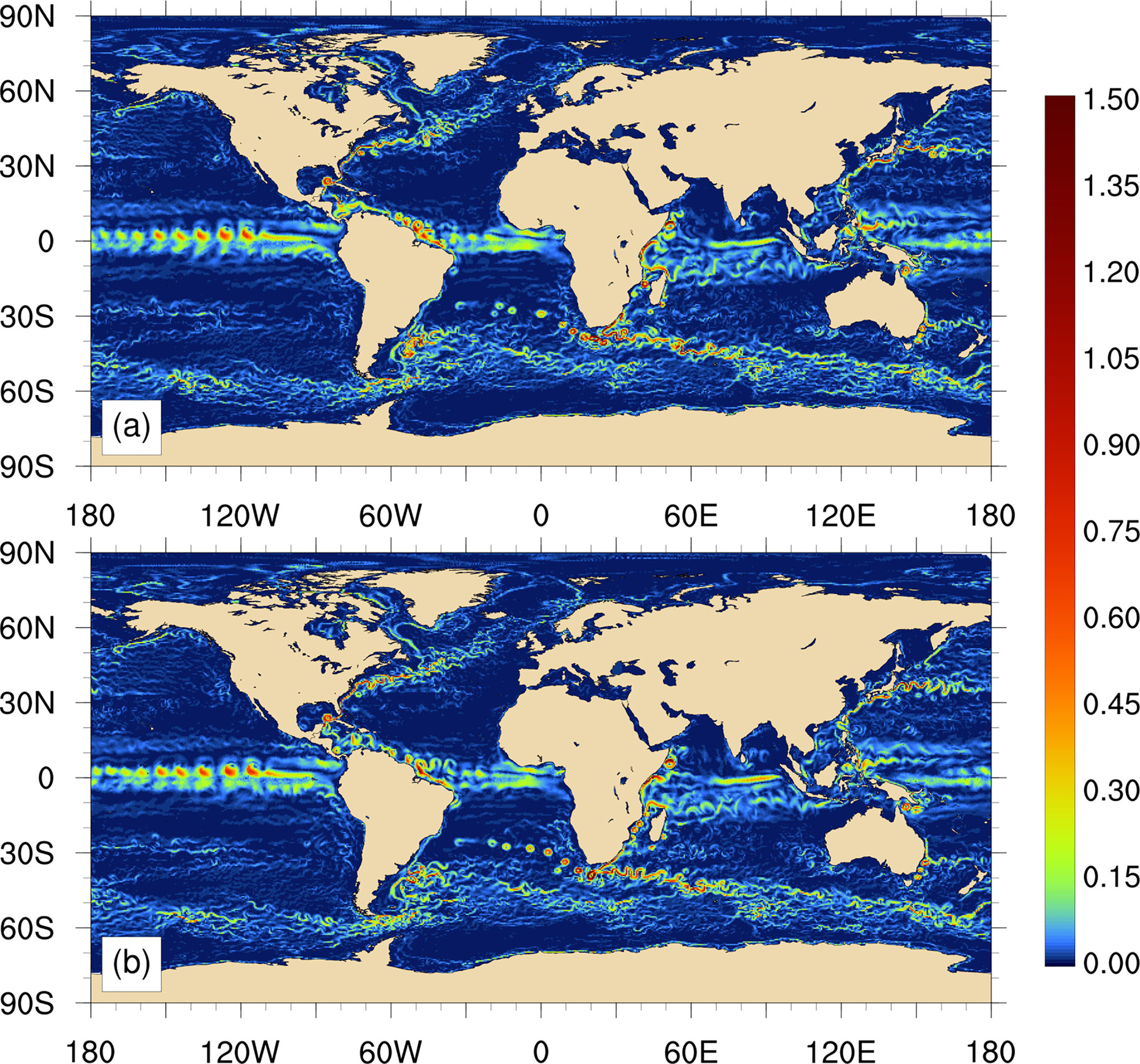
This study shows the possibility of using the semi-implicit time-stepping algorithm in the MPAS-O through several test case experiments using a range of processor counts. The semi-implicit barotropic mode solver has better computational efficiency than the existing split-explicit subcycling scheme without degrading the accuracy (Fig. 1). This new semi-implicit version of the MPAS-O can allow researchers to simulate their numerical experiments using the MPAS-O standalone as well as the integrated E3SM faster with more desirable stability.
Summary
A scalable semi-implicit barotropic mode solver for the ocean component of the model for prediction across scales has been implemented as a competitor to an existing explicit-subcycling scheme to allow faster and more stable simulations while not sacrificing accuracy. The semi-implicit solver adopts the pipelined preconditioned bi-conjugate gradient stabilization algorithm as an iterative solver in conjunction with the restricted additive Schwarz preconditioner that accelerates the convergence rate of the iterative solver. The preconditioner is constructed from a linearized barotropic system that also reorders the system for optimal performance, while the semi-implicit solver deals with the fully nonlinear barotropic system that requires reassembly of the coefficient matrix for every time step. Several numerical experiments, from simple one-dimensional tests to three-dimensional real-world tests (Fig 2,3), demonstrate that the semi-implicit solver has almost the same accuracy and better parallel scalability compared with the existing scheme while allowing faster and more stable simulations. Furthermore, the semi-implicit solver accelerates the barotropic mode up to 2.9 times faster than the existing scheme on 16,320 processors, leading to an overall runtime speedup of 1.9.
Figure 2. Snapshots of surface kinetic energy (m(-2)s(-2)) at day 800 using the realistic simulation for the semi-implicit (a) and explicit-subcycling (b) version of the MPAS-O. MPAS-O, Model for Prediction Across Scales-Ocean.
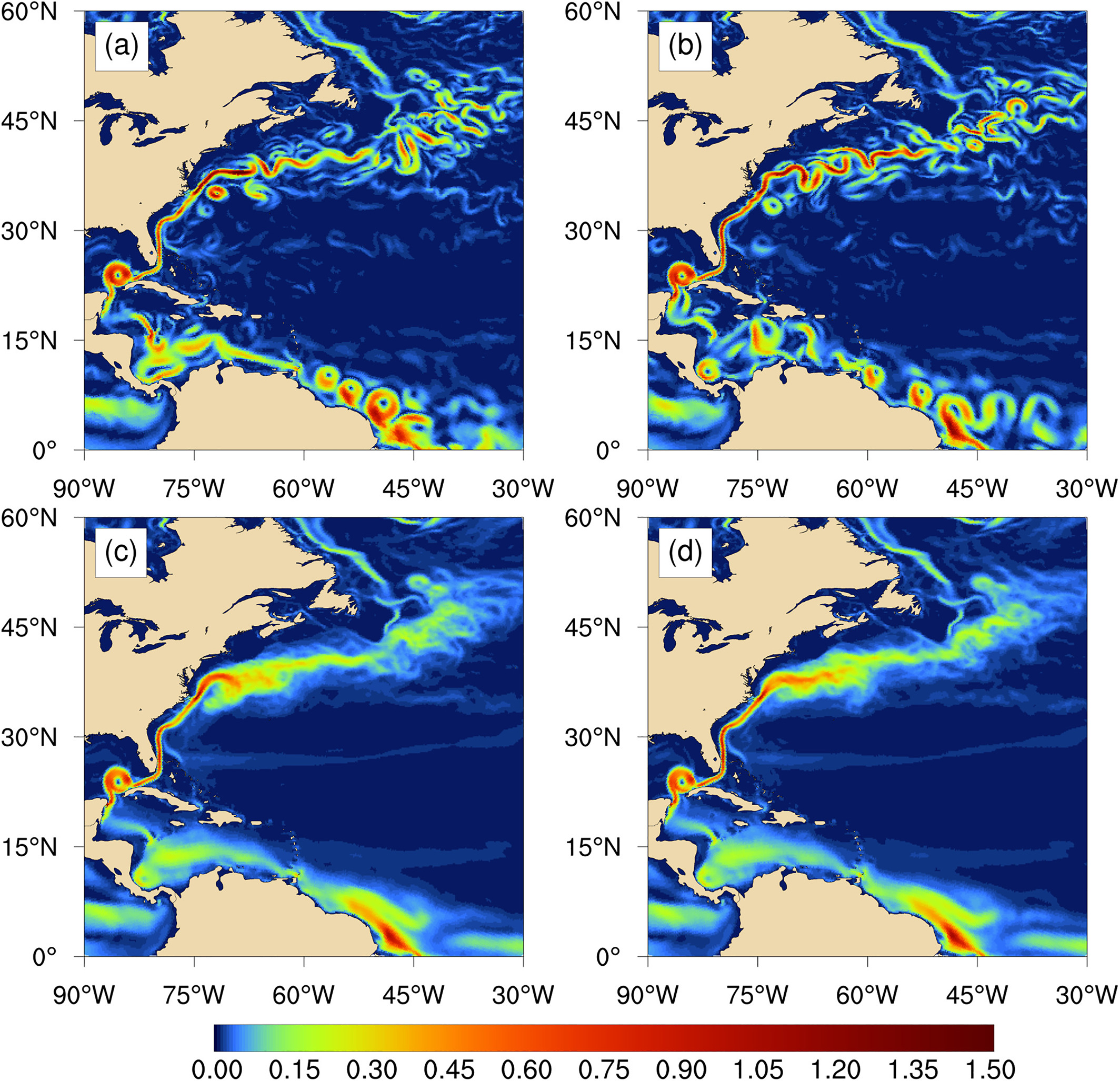
Figure 3. Zoomed views of snapshots of surface kinetic energy as in Fig.2 (top row; a and b) and mean fields (bottom row; c and d) in Northwest Atlantic Ocean for the semi-implicit (left column; a and c) and explicit-subcycling (right column; b and d) version of MPAS-O. MPAS-O, Model for Prediction Across Scales-Ocean.
Publication
- Kang, H, KJ Evans, MR Petersen, PW Jones, and S Bishnu. 2021. “A Scalable Semi‐Implicit Barotropic Mode Solver for the MPAS‐Ocean.” Journal of Advances in Modeling Earth Systems 13(4). https://doi.org/10.1029/2020ms002238.
Funding
- This work was supported by the Earth System Model Development program in the US Department of Energy, Office of Science, Office of Biological and Environmental Research.
Contact
- Hyun-Gyu Kang, Oak Ridge National Laboratory
