Parallel Exponential Time Differencing Methods for Geophysical Flow
The Science
Multi-layer shallow water equations and primitive equations are commonly employed to predict geophysical flows when stratification effects are taken into account. The scientists designed and implemented parallel exponential time differencing (ETD) methods for time integration of these equations based on domain decomposition to speed up their numerical simulations. Specifically, exponential Rosenbrock-Euler (Hochbruck et al., 2009), ETD2wave, and B-ETD2wave (Pieper et al., 2019) schemes are implemented for the multi-layer shallow water equations. The ETD method is also applied to solve the (fast) barotropic mode, instead of the explicit sub-stepping process currently implemented in MPAS-Ocean, within the baroclinic-barotropic splitting approach for the multi-layer primitive equations.
Figure 1. Shallow water equations (the SOMA test): simulated surface velocities on Day 15 and their numerical errors produced by the ETD methods (left: exponential Rosenbrock-Euler, center: ETD2wave, right: B-ETD2wave) and the results of computational times and parallel efficiencies.
The Impact
This work shows the great potential of applying parallel ETD methods for simulating real-world geophysical flows. First, the proposed parallel ETD methods obtain good parallel scalability for the shallow water equations and the primitive equations. Second, compared to existing models in MPAS-Ocean, the proposed methods can result in lower computational costs to achieve similar accuracies.
Summary
The multi-layer shallow water equations and the multi-layer primitive equations are considered for geophysical flow simulations. For the former, this study investigates the parallel performance of exponential time differencing methods, including exponential Rosenbrock-Euler, ETD2wave, and B-ETD2wave schemes. For the latter, the proposed work takes advantage of the splitting of barotropic and baroclinic modes and designs a new two-level method in which the ETD method is applied to solve the (fast) barotropic mode. These methods improve the computational efficiency of numerical simulations for geophysical flows because ETD schemes allow for much larger time step sizes than traditional explicit time-stepping schemes popularly used in existing computational ocean models.
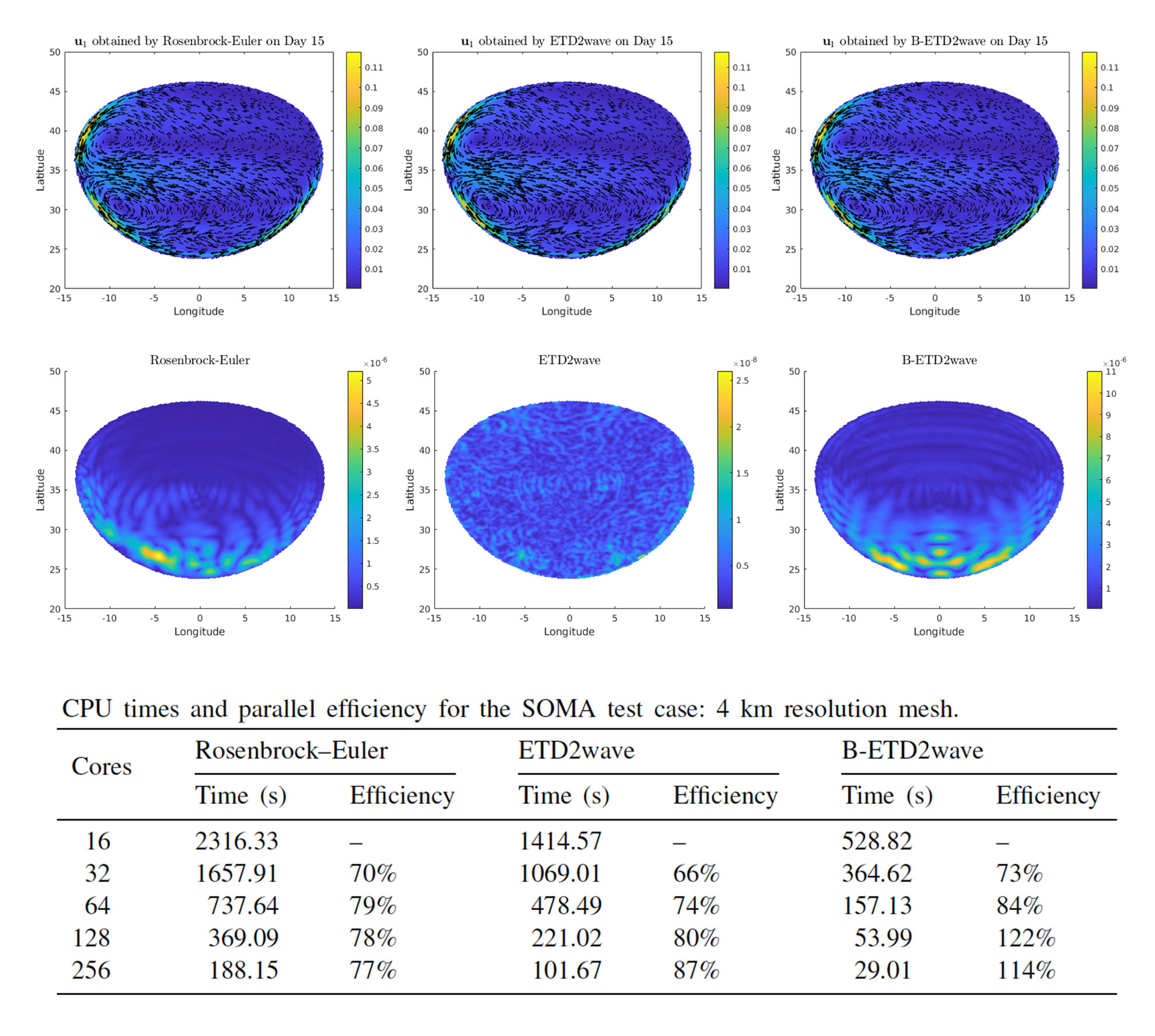
Several benchmark tests for ocean modeling were carried out to demonstrate the performance and parallel scalability of the proposed ETD methods. Fig. 1 presents simulation results of the SOMA test governed by shallow water equations. Rosenbrock-Euler, ETD2wave, and B-ETD2wave all produce similar simulation results for surface velocity. In terms of computational performance, for all the cases using different number of cores, B-ETD2wave is the most efficient one, and its efficiency monotonically increases along with the number of cores but levels off for more than 128 Cores. Fig. 2 presents simulation results of the global ocean circulation test which is governed by primitive equations. The SE2 method currently adopted in MPAS-Ocean obtains better parallel efficiencies for all different number of cores, but the ETD-SE2 method uses less computational times in all cases.
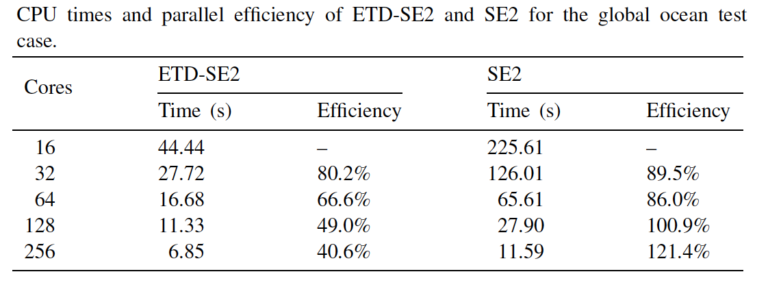
Figure 2. Primitive Equations (the global ocean circulation test): simulated surface increments of salinity and temperature produced by the ETD-SE2 method, and the results of computational times and parallel efficiencies for the barotropic solve in comparison with the SE2 method (currently adopted in MPAS-Ocean).
Publication
R. Lan, W. Leng, Z. Wang, L. Ju, and M. Gunzburger. 2021. “Parallel exponential time differencing methods for geophysical flow simulations’’. Computer Methods in Applied Mechanics and Engineering, 387, 114151. https://doi.org/10.1016/j.cma.2021.114151
Funding
- The U.S. Department of Energy Office of Science, Biological and Environmental Research Program supported portions of this research as part of the Regional and Global Model Analysis (RGMA), Atmospheric System Research (ASR), and Earth System Model Development (ESMD) program areas.
- This research used resources of the National Energy Research Scientific Computing Center (NERSC).
- This research has been supported by the Scientific Discovery through Advanced Computing (SciDAC) and Earth System Model Development (ESMD) via the “Efficient and scalable time-stepping algorithms and reduced-order modeling for ocean system simulations” project
Contact
- Lili Ju, University of South Carolina
